Skip to content

ARIMA Models Identification: Correlograms

Last Update: June 20, 2022

ARIMA Models Identification: Correlograms are used to identify ARIMA models autoregressive and moving average orders.

As example, we can delimit univariate time series y_{t} into training range y_{t(a)} for model fitting and testing range y_{t(b)} for model forecasting.

Then, we can do training range univariate time series ARIMA(p,d,q) model autoregressive p and moving average q orders identification by estimating sample autocorrelation and partial autocorrelation functions correlograms. Notice that we need to evaluate whether level or d order differentiated training range univariate time series is needed for ARIMA model integration d order.

Next, we estimate training range univariate time series sample autocorrelation function correlogram with formula \hat{\rho}_{h}=\frac{\sigma\left ( y_{t(a)},y_{t(a)-h} \right )}{\sigma^{2}_{y(a)}}\:(1). Training range univariate time series estimated lag h sample autocorrelation function \hat{\rho}_{h} is the estimated sample covariance between univariate time series y_{t(a)} and its lag h univariate time series y_{t(a)-h} divided by univariate time series estimated sample variance \sigma^{2}_{y(a)} . Training range autocorrelation function is the linear dependence between current y_{t(a)} and lagged y_{t(a)-h} univariate time series data.

After that, we estimate training range sample autocorrelation function correlogram confidence intervals with formula ci_{h}=\pm n^{-1}\left ( 1-\frac{\alpha}{2} \right )\sqrt{\frac{1+2\sum_{i=1}^{h-1}\hat{\rho}_{i}^{2}}{n(a)}}\;(2). Training range sample autocorrelation function confidence intervals ci_{h} are the inverse of the standard normal cumulative distribution n^{-1} with probability equal to one minus statistical significance level \alpha divided by two and this result multiplied by the square root of one plus two times the sum of sample autocorrelation function square values \hat{\rho}^{2}_{i} divided by number of observations n(a). Notice that we need to evaluate whether Bartlett formula is needed for sample autocorrelation function correlogram confidence intervals estimation.

Later, we estimate training range univariate time series sample partial autocorrelation function correlogram with formula \hat{\phi }_{h}=\hat{\beta}_{h}\;(3). Training range univariate time series lag h sample partial autocorrelation function \hat{\phi}_{h} can be estimated through lag h linear regression estimated coefficient \hat{\beta}_{h} with formula \hat{y}_{t(a)}=\hat{\beta}_{0}+\sum_{i=1}^{h}\hat{\beta}_{i}y_{t(a)-i}\;(4). Training range partial autocorrelation function is the linear dependence between current y_{t(a)} and lagged y_{t(a)-h} univariate time series data after removing any linear dependence on y_{1(a)},...,y_{t-h+1(a)}. Notice that we can also estimate sample partial autocorrelation function using Yule-Walker, Levison-Durbin or adjusted linear regression methods.

Then, we estimate training range sample partial autocorrelation function correlogram confidence intervals with formula ci_{h}=\pm n^{-1}\left ( 1-\frac{\alpha}{2} \right )\left ( \frac{1}{\sqrt{n(a)}} \right )\;(5). Training range sample partial autocorrelation function confidence intervals ci_{h} are the inverse of the standard normal cumulative distribution n^{-1} with probability equal to one minus statistical significance level \alpha divided by two and this result multiplied by one divided by the square root of number of observations n(a).

Next, we can do training range univariate time series ARIMA(p,d,q) model autoregressive p and moving average q orders identification.

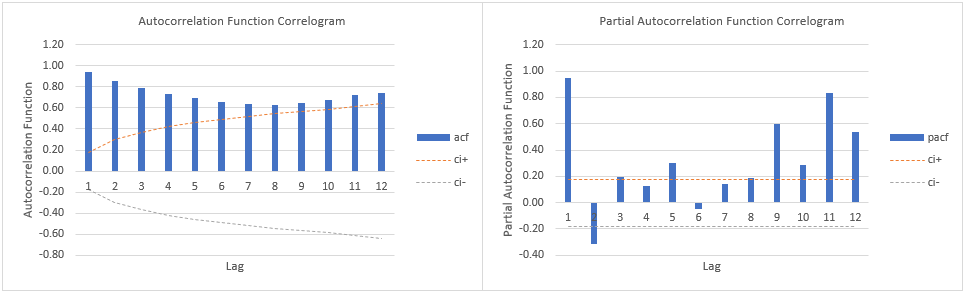
  • If sample autocorrelation function correlogram \hat{\rho}_{h} tails of gradually and sample partial autocorrelation function correlogram \hat{\phi}_{h} drops after p statistically significant lags then we can observe the potential need of an autoregressive model AR(p) of order p.
  • Alternatively, if sample autocorrelation function correlogram \hat{\rho}_{h} drops after q statistically significant lags and sample partial autocorrelation function correlogram \hat{\phi}_{h} tails off gradually then we can observe the potential need of a moving average model MA(q) of order q.
  • Otherwise, if sample autocorrelation function correlogram \hat{\rho}_{h} tails of gradually after q statistically significant lags and sample partial autocorrelation function correlogram \hat{\phi}_{h} tails off gradually after p statistically significant lags then we can observe the potential need of an autoregressive moving average model ARMA(p,q) of orders p and q.

Below, we find example of training range univariate time series ARIMA(p,d,q) model autoregressive p and moving average q orders identification correlograms using airline passengers data [1]. Training range as first ten years and testing range as last two years of data. Correlograms confidence intervals with \alpha=5% statistical significance level. Notice that correlograms confidence intervals statistical significance level was only included as an educational example which can be modified according to your needs.

Figure 1. Microsoft Excel® training range univariate time series ARIMA(p,d,q) model autoregressive p and moving average q orders identification correlograms using airline passengers data.

References

[1] Data Description: Monthly international airline passenger numbers in thousands from 1949 to 1960.

Original Source: Box, G. E. P., Jenkins, G. M. and Reinsel, G. C. (1976). “Time Series Analysis, Forecasting and Control”. Third Edition. Holden-Day. Series G.

Source: datasets R Package AirPassengers Object. R Core Team (2021). “R: A language and environment for statistical computing”. R Foundation for Statistical Computing, Vienna, Austria.

My online courses are closed for enrollment.
+