Last Update: February 21, 2022
Homogeneity of Regression Slopes is when linear regression intercept and slopes are homogeneous across populations. This can be tested through Wald test which adds as dummy independent variables and dummy independent variables products with independent variables to model equation and evaluates whether there are changes in intercept and slopes across populations. If there are changes in intercept and slopes across populations, then they are not homogeneous.
As example, we can fit a three-variable restricted multiple linear regression with formula . Then, as example again, we can fit a four-variable unrestricted multiple linear regression by adding dummy independent variable
and dummy independent variable
products with independent variables
with formula
. Next, we can do Wald test with joint null hypothesis that dummy independent variable
and dummy independent variable products with independent variables
coefficients are equal to zero with formula
. If joint null hypothesis is rejected, then restricted multiple linear regression (1) intercept and/or slopes are not homogeneous across populations. Notice that joint null hypothesis test (3) would require additional individual coefficients tests to evaluate which restricted multiple linear regression (1) intercept and/or slopes are not homogeneous across populations. Also, notice that dummy independent variable is a qualitative variable converted into a binary quantitative variable with values of one for specific population classification and zero otherwise.
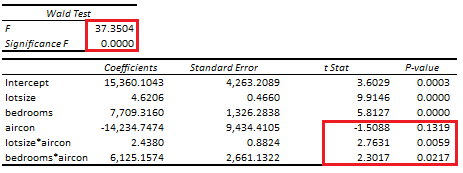
Below, we find an example of unrestricted multiple linear regression of house price explained by its lot size, number of bedrooms, air conditioning as dummy independent variable coefficients and homogeneity Wald test [1]. Notice that air conditioning dummy independent variable was converted from a qualitative variable into a binary quantitative variable with values of one for category yes and zero for category no.
Courses
My online courses are hosted at Teachable website.
For more details on this concept, you can view my Linear Regression Courses.
References
[1] Data Description: Sales prices of houses sold in the city of Windsor, Canada, during July, August and September, 1987.
Original Source: Anglin, P., and Gencay, R. (1996). Semiparametric Estimation of a Hedonic Price Function. Journal of Applied Econometrics, 11, 633–648.
Source: AER R Package HousePrices Object. Christian Kleiber and Achim Zeileis. (2008). Applied Econometrics with R. Springer-Verlag, New York.