Last Update: February 21, 2022
Normality in Error Term is when linear regression errors are normally distributed. This can be visually tested through Q-Q plot or quantile-quantile plot which evaluates whether points comparing linear regression residuals sample quantiles and normal distribution theoretical quantiles are within points regression line fit. If points are outside their regression line fit, then model errors are assumed non normally distributed. This can also be tested through Jarque-Bera test [1] which evaluates whether model residuals skewness and excess kurtosis are equal to zero. If model residuals skewness and excess kurtosis are different to zero, then model errors are assumed non normally distributed.
As example, we can fit a three-variable multiple linear regression with formula . Then, we can obtain regression residuals
with formula
which are the estimated differences between actual
and fitted
values.
Next, we can do Q-Q plot with points comparing residuals in ascending order on vertical axis as sample quantiles and inverse of standard normal cumulative distribution function at ascending order ranks percentiles on horizontal axis as theoretical quantiles. After that, we can do points regression line fit and visually test whether points are outside of it. If points are outside their regression line fit, then regression (1) errors are assumed non normally distributed. Notice that Q-Q plot reference line can be points regression line fit, quantiles regression line fit or 45-degree line.
Below, we find example of residuals normal Q-Q plot from multiple linear regression of house price explained by its lot size and number of bedrooms [2].
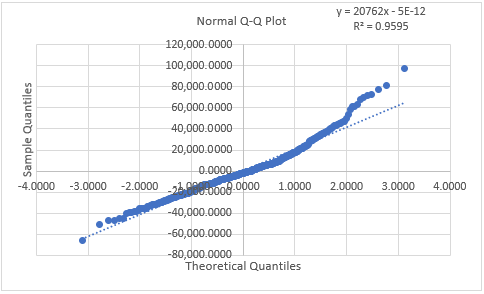
Later, we can do Jarque-Bera test with test statistic formula where
is residuals number of observations,
is residuals sample skewness,
is residuals sample excess kurtosis and chi-square test with joint null hypothesis that residuals skewness and excess kurtosis are equal to zero with formula
. If joint null hypothesis is rejected, then regression (1) errors are assumed non normally distributed.
Below, we find example of residuals Jarque-Bera test from multiple linear regression of house price explained by its lot size and number of bedrooms [2].
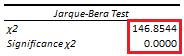
Courses
My online courses are hosted at Teachable website.
For more details on this concept, you can view my Linear Regression Courses.
References
[1] Jarque, Carlos M.; Bera, Anil K. (1987). “A test for normality of observations and regression residuals”. International Statistical Review. 55 (2): 163–172.
[2] Data Description: Sales prices of houses sold in the city of Windsor, Canada, during July, August and September, 1987.
Original Source: Anglin, P., and Gencay, R. (1996). Semiparametric Estimation of a Hedonic Price Function. Journal of Applied Econometrics, 11, 633–648.
Source: AER R Package HousePrices Object. Christian Kleiber and Achim Zeileis. (2008). Applied Econometrics with R. Springer-Verlag, New York.